电脑音频虚拟仪器的构建与使用（二）

发表评论

A+

4.音频测试项目简介

4.1. FFT

首先介绍一个最重要的概念：FFT，即快速傅立叶变换，上述软件的许多测试项目都是基于快速傅立叶变换分析的结果。这是现代电子学频谱分析的常规手段，特别是引入计算机技术后，更是方便快捷而且直观精确的不二选择。简单讲，一般信号波形的记录都是以时间-幅度相关的形式直观表现出来的，称为时域分析；而快速傅立叶变换就是分析计算信号波形中的频谱成分强度，将其能量从时间积分，从而得出频率-能量相关的形式，称为频域分析。注意这里讲的是频率-能量相关，而非一般认为的频率-幅度相关，因为傅立叶变换实际上已经无法确认信号不同频率间的幅度关系，而只能计算出其能量关系。理解这一点对理解快速傅立叶变换分析的结果很重要，据笔者所知大部分教科书或工具辞书都没有讲明这一点，软件的帮助文件也常常做出频率-幅度相关的错误解释，所以提请读者注意。

对于完全随机分布的信号，例如白噪声、粉红噪声，其每一频段能量平均分布在所有时段，因此与振幅是完全成正比的，故而FFT分析的结果称为频率-幅度关系也是可以的；但对于那些各频段能量分布随时间变化的信号，例如对数扫频信号、一般的语音、音乐，就不能这样理解了，事实上它们的高频部分振幅与低频相同或甚至更高，但FFT分析的结果却是低于低频的，因为它们占的时间比例小，这时必须用能量的观点去理解，否则会令人困惑，这是笔者长时间学习和分析思考得出的结论。

在用Spectra和Adobe Audition进行扫频测试时，上述思路会对我们分析和做结论有所帮助。例如对数扫频的振幅实际是恒定的，但FFT分析的结果为-3dB/oct衰减（oct：octave，八度音，倍频程）。

4.2.频率响应测试

频率响应的平直与否直接关系到重放频带的范围以及重放信号的保真度。对于所有电声设备，频率响应无疑是最基本的指标，因而成为所有测试项目中最基本的一项。传统的频率响应测量大多采用扫频/点频信号或白噪声/粉红噪声信号，电路测试比较简单，只需将待测设备接入回路并调节好回路电平即可，声学测量大多在专业消声室进行。由于消声室构造复杂投资大而难以普及，近几十年开发了许多适用于普通房间环境的测试方法和测试系统，其基本原理一般都是用一个合适的时间窗口来接受信号，其它时间关闭以舍去反射的影响。近年来计算机技术的进步使得复杂的程序和计算得以快速完成，FFT分析普遍使用。现在几乎所有的专业测试系统都是基于计算机的，大多具有时间窗口功能，可以在普通环境进行声学测试，比较好的系统具有脉冲响应FFT分析和前/后沿累积频谱三维显示功能，能够对电声器材的特性进行更全面和深刻的反映。

这些系统当然都是相当昂贵的，不过本文介绍的软件可以完成所有类似的测试项目。

先说噪声测试，即用白噪声、粉红噪声作测试信号。Spectra和Adobe Audition都可以产生精确的噪声，而RMAA的普通测试模式为一段类白噪声，频带范围为5Hz至1/2取样频率，其实质是一系列点频的混合，在1KHz至10KHz间最密集，而且其高低频都有衰减，其目的是与实际的音乐频谱尽量接近，并不是严格的白噪声。

再看扫频测试。Spectra和Adobe Audition都可以自己定义扫频特性，特别是Adobe Audition，可以非常自由地产生想要的信号。RMAA的声学测量模式为20至20000Hz的对数扫频，但与Spectra和Adobe Audition的分析方法有所不同，正常的结果是完全平直的。

脉冲响应测试和FFT分析需要Spectra和Adobe Audition配合，也可以称为“瞬态响应”，放到5.4节讨论。

4.3.信噪比

信噪比是反映器材质量的又一重要指标，由器材产生的与输入信号无关的信号都是噪声。信噪比指的是设备能够处理的最大信号与噪声的比值，一般以最大信号为0dB，噪声用负分贝值表示，即在最大不失真信号的若干分贝以下，取正值就是信噪比。噪声大的设备会将小信号淹没，丢失许多信号细节，因此噪声应该越小越好。噪声也是有频带的，有时可能频带很宽，但我们计量时一般只取音频范围，而且要用人耳的敏感曲线（A计权）去均衡，可以得到实用的，也是更好看的噪声指标。例如-120dB的噪声表示噪声有效值是最大不失真信号的百万分之一，差不多是现代声卡、放大器所能达到的最好水平。而-80dB的噪声表示噪声有效值是最大不失真信号的一万分之一，只能算一般水平。

噪声的测量是比较简单的，只需测量无输入信号时的输出电平即可，不过要注意应该将设备的增益调节到最大不失真状态，否则会给出虚假的高指标。这在任何测试系统里都是一样的。

在用FFT分析时可以引入“分段噪声”的概念，与我们听音的要求是不一样的。例如某系统的噪声是-85dBA，那么一般认为-85dB以下的信号就无法还原了。但事情并没有那么简单，-85dBA的噪声到底是由哪些频段产生的呢？

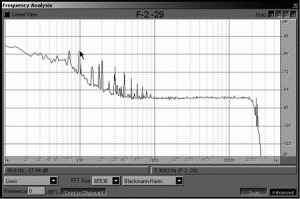
图4

让我们看一看噪声频谱分析的情况。如图4，这是一个典型的主板集成声卡的噪声频谱，由Adobe Audition分析出的结果。RMAA测试的结果为噪声水平-53.0dBA，可以说是相当差的结果，而且二者是吻合的。由图中我们可以看出，其噪声能量大部分分布在300Hz以下，而且主要是由50Hz和75Hz的谐波产生的，可以推断是交流电源和显卡的干扰造成的，而其余频段则能量小得多，到1KHz以上都在-86dB以下。这就是“分段噪声”的体现。

怎么理解上述的分析结果呢？简单的办法就是将上述曲线看作“掩蔽曲线”（峰谷多的地方取峰值顶点连线），凡是频谱在此曲线以下的信号都是不可能正确还原的，而不是简单的所有低于-53.0dB的信号。比如在1KHz以上-80dB的信号就可以还原（当然质量不高），由FFT分析检测出来，实际上人耳也有类似的检测能力，只不过由于掩蔽效应，灵敏度比计算机的精确FFT分析要低很多。

4.4.动态范围

动态范围是指设备能够处理的最大信号与最小信号的比值。这个概念容易与“信噪比”的概念混淆，那么二者有什么区别呢？可以理解，小于噪声幅度的信号是无法正确还原的，但是有的设备能够在无信号或信号特别低时从某些环节将噪声连同小信号切除，从而得出更好的信噪比指标（这就是“动态降噪”的基本原理）。这时实质上还是无法正确处理小信号的，而动态范围的测量就可以避免这样的人为优化。动态范围的测量是用一个小信号（一般用-60dB/1000Hz的正弦波）输给设备，然后滤除信号，测量其余频率的噪声和谐波水平，再用最大信号与之相比，结果就是动态范围。

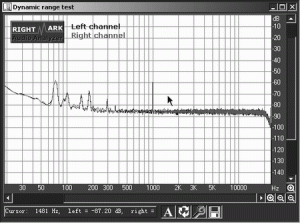
可以预见动态范围一般要低于信噪比，但在没有特殊电路或软件处理噪声的情况下，一般二者差距不大，可以互相参考。图5给出了动态范围测试的结果。这里基本没有产生大于噪声的谐波，因此动态范围和信噪比是基本一样的。

图5

需要指出，测量出的动态范围与“理论上”的动态范围是不同的。例如现在的数字音源，大多用数字信号能够还原的理论值来标注，例如CD的动态范围96 dB，DVD采用24bit记录能达到144dB！实际上由于模拟器件的限制，那样的指标是根本不可能实现的，你只需测试一下其噪声水平就知道了。只不过目前音像节目后期制作大部分都是用计算机数字处理的，在许多环节的处理过程中用高比特可以尽量避免信号劣化。（实际上甚至可能用48bit量化来处理！）

4.5.总谐波失真THD

总谐波失真是指由输入信号激发的其它频率的能量总和，是典型的非线性失真。其测量方法是输入一个强信号（一般为-3dB/1000Hz，略低于最高值，防止削顶而产生大量谐波），然后测量其余频率的总能量与信号能量的比值。可以理解，总谐波失真越小，设备的保真度越高，信号的纯度越高。特别对于晶体管电路，其谐波成分大部分为奇次即基波的3、5、7倍，失真大时使声音发毛刺耳，很不耐听，因此该指标值越小越好。而电子管电路有些例外，其谐波成分以偶数为主，结果使声音显得温暖、甜润，结果虽然失真较大却挺讨人喜欢，但这已涉及到人的主观感受而不是严格的高保真概念了。

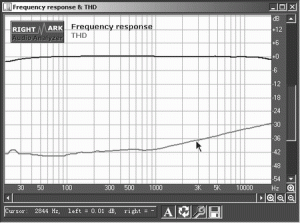
传统的测试方法THD只测1000 Hz，这其实是远远不够的，许多设备在不同的频段THD值差别很大，特别是在电声测试时，一个频点根本不可能反映全貌。好在这里介绍的三个软件都可以方便地改变THD测试信号的频率并很快得出希望的计算结果，特别是RMAA的声学测量同时附带全音频范围THD测量功能（实际可以单测2、3次谐波，也可以是THD+N，即包含噪声），可以生成一条THD曲线，如图6所示为THD+N，直观地显示出THD变化的规律。